

¿Cómo definimos el color “exacto”? ¿Cómo podríamos cuantificar el color de una manera “precisa”? Antes de entrar en este tema, hablemos un poco más de por qué la cuantificación del color es importante para los fotógrafos, los diseñadores, los profesionales de la imagen, las personas en industrias textiles y más.
Cuando intentamos describir un color, la forma más común de hacerlo es referirnos a un objeto con el color en mente. Por ejemplo, cuando describimos el color “rojo”, la gente usualmente usa “manzana” para describir el “rojo”. Pero, ¿de qué tipo de manzana estamos hablando? ¿Estamos pensando en la misma manzana? Mira la Figura 1, hay al menos siete tonos diferentes de “rojo” entre las diferentes variedades de manzana. Sin mencionar el último; ¡ni siquiera es rojo! Por lo tanto, hay discrepancias cuando usamos objetos para describir colores. Y necesitamos encontrar una forma de reducir las discrepancias en una comunicación.

Figura 1: Diferentes variedades de manzanas
Los humanos tienden a usar “números” para expresar una medida precisa. Por ejemplo, utilizamos números para describir la longitud, el peso, etc., por lo tanto, necesitamos una manera de expresar los colores en formas numéricas, así que podríamos decir que el color A y el color B son iguales porque tienen los mismos valores numéricos. En 1913, la CIE (Commission Internationale de l'Eclairage) definió los valores triestímulos (valores XYZ) para cuantificar los colores que los humanos pueden percibir. Los valores XYZ se construyen multiplicando los siguientes tres atributos: la distribución de potencia espectral de la fuente de luz, la reflectancia del objeto y las funciones del Observador Estándar para describir las características del sistema visual humano. Como resultado, cuando el color A y el color B tienen los mismos valores XYZ, podríamos decir que el color A y el color B se ven iguales.
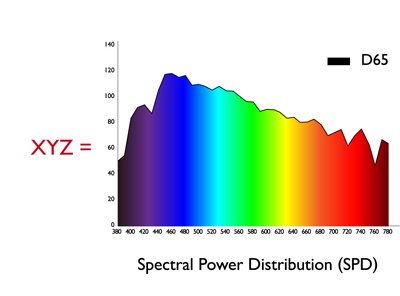
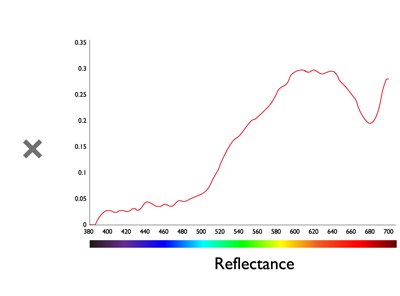
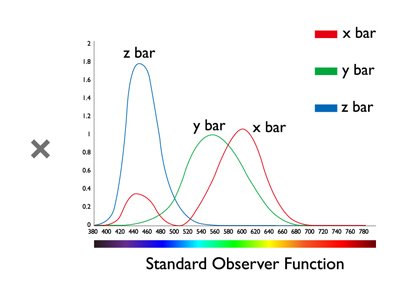
Figura 2: Fórmula para calcular los valores XYZ
Otra ventaja de definir colores en valores numéricos es que podríamos expresar colores fácilmente en un diagrama con un sistema de coordenadas. Y esto forma un espacio de color. La Figura 3 muestra el Diagrama de cromaticidad xy CIE de 1931, que representa todos los colores que los humanos podrían percibir. Sin embargo, este diagrama no refleja realmente la sensibilidad del sistema visual humano. Toma el azul y el verde, por ejemplo. Los humanos son muy sensibles al azul y menos sensibles al verde: un poco más de rojo lo reconocemos como púrpura, y un poco de verde lo reconocemos como cian. Este fenómeno no se refleja en la Figura 3, un diagrama de cromaticidad CIE 1931 xy. Como resultado, en 1976, se propuso el diagrama de cromaticidad u’ v’ para reflejar la sensación del sistema visual humano.
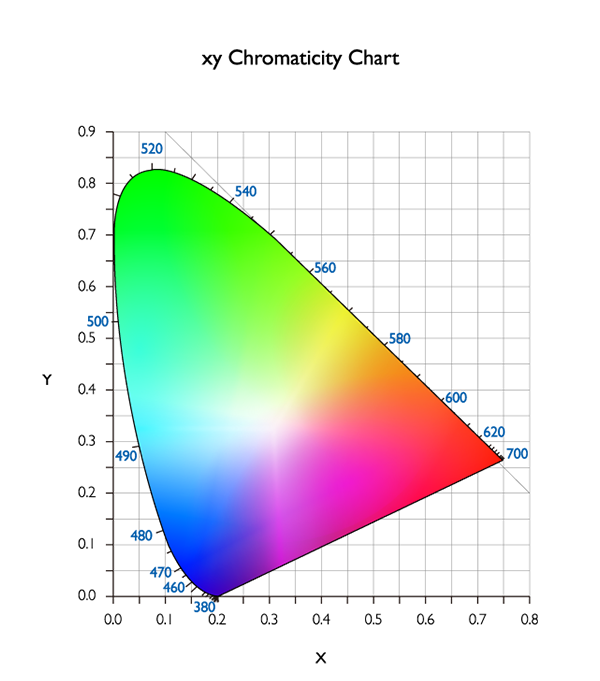
Figura 3: Diagrama de cromaticidad CIE 1931 xy
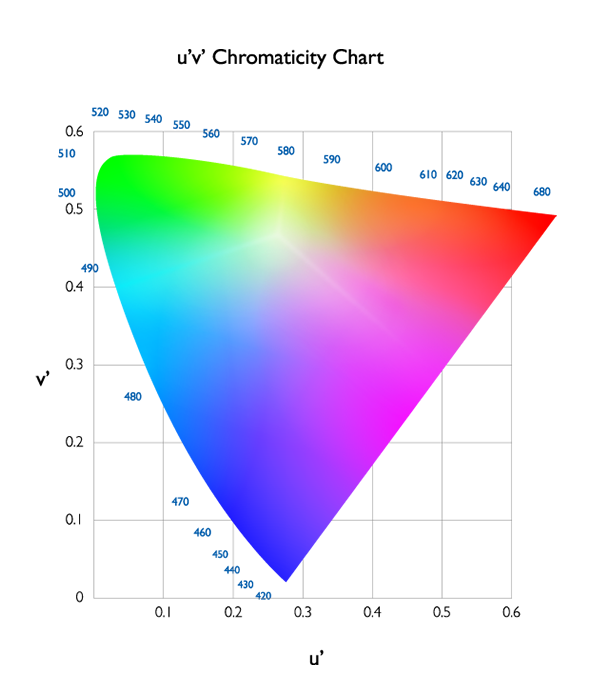
Figura 4: Diagrama de cromaticidad CIE 1976 u’v’
Ahora, hemos definido un sistema para describir los colores en forma numérica.
Podríamos usar una regla para medir la longitud y usar una báscula para medir el peso. Cuando medimos colores, primero tenemos que medir la luz. Medir la luz no es tan fácil como usar una regla o una báscula, pero hay instrumentos que nos ayudan. Por ejemplo, podríamos usar un espectrorradiómetro para medir la distribución de potencia espectral de la luz.
Sin embargo, estos instrumentos son voluminosos y costosos, y no son fáciles de transportar. Por lo tanto, se desarrolló un dispositivo más simplificado llamado “colorímetro”. Un colorímetro mide la luz a través de un conjunto de filtros XYZ, por lo que su velocidad es más rápida que el espectrorradiómetro, pero con menos precisión.
* Filtros XYZ: Filtros ópticos para imitar las características ópticas de los valores XYZ (valores triestímulos) en términos de transmitancia por longitud de onda.
Como se dijo anteriormente, cuando tenemos un conjunto de valores XYZ con los mismos números, podríamos decir que estos colores se ven iguales. Pero hay ocasiones en que los valores XYZ no son los mismos, pero aún se ven muy similares. Por ejemplo, cuando vemos una luz brillante en una habitación luminosa en comparación con una luz más tenue en una habitación poco iluminada, los valores XYZ medidos no son los mismos (debido a las diferentes intensidades de luz, pero aún así percibimos el mismo color de la luz). Esto se debe a la adaptación de nuestro sistema visual. Otro escenario es comparar los colores de diferentes medios. Por ejemplo, uno del monitor y otro del papel impreso. Por lo tanto, necesitamos otra medida para cuantificar este fenómeno de adaptación. Espacio de color L*a*b* (que se muestra en la Figura 5) fue luego propuesto y construido para este propósito de “normalización”. Define el nivel de luz más brillante en una escena o un medio (por ejemplo, papel) como 100, y normaliza todos los demás colores en la escena o los medios de acuerdo con la luz más brillante. Como resultado, ahora podemos comparar la luz con diferentes intensidades o colores de diferentes medios.
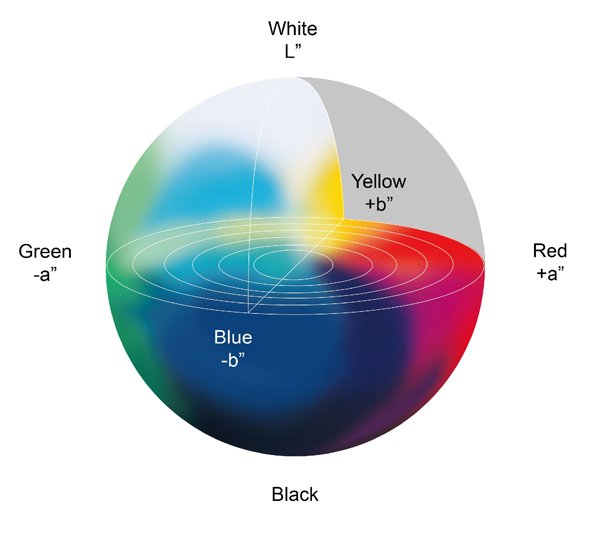
Figura 5: Espacio de color L*a*b*
Cuando vemos dos colores similares, pero ligeramente distintos, nos preguntaremos ¿qué tan cerca están estos colores? Sin usar valores numéricos para representar colores, podríamos decir “está cerca”. Pero, ¿qué tan cerca? Y cuál es la definición de “cerca” ya que la percepción de los colores varía de una persona a otra. Con el espacio de color XYZ o el espacio de color L*a*b*, podemos cuantificar la diferencia entre los colores. Al calcular la distancia entre dos colores en un espacio de color en particular (normalmente se usa el espacio de color L*a*b*), se puede obtener un valor de diferencia. Este valor de diferencia se llama “Diferencia de color”. Usamos el delta E* para designar “Diferencia de color”.
La versión más simple de la fórmula de diferencia de color se llama delta E*76 (delta E*ab).
Una fórmula más compleja se usa en la industria textil y de artes gráficas. Fue anunciado en 1994, por lo tanto, se llama delta E*94.
En el año 2000, los investigadores desarrollaron una versión más nueva de la fórmula de diferencia de color para reflejar realmente lo que el sistema visual humano percibe. Se llama delta E * 2000 (delta E * 00). Debido a la gran cantidad de estudios de investigación para lograr una alta correlación entre los valores calculados y la percepción humana, delta E*00 se ha convertido en Norma Internacional, y se recomienda usar en todo el trabajo de investigación científica.
Como hemos visto en las fórmulas anteriores, se requieren dos conjuntos de valores L*a*b*. Si necesitamos juzgar la precisión de un color en particular, entonces se requiere un conjunto de valores medidos de L*a*b* y un conjunto de valores definidos de L*a*b*. Podríamos obtener los valores medidos utilizando los instrumentos mencionados anteriormente, pero ¿cómo obtenemos valores “definidos” o “estándar”? Los valores “definidos” o “estándar” se pueden obtener utilizando gráficos estándar (Figura 6). Estas tablas de colores tienen valores L*a*b* definidos para todos los colores en la tabla, y cada tabla se elabora con mucho cuidado para cumplir con la tolerancia. Por lo tanto, estos gráficos podrían usarse como referencia ya que los valores no cambiarán.
Para juzgar la precisión de un color, con frecuencia se usa delta E * 00. Delta E * 00 < 1.00 significa que no hay una diferencia perceptible para los expertos al comparar dos colores uno al lado del otro. Delta E * 00 < 3.00 significa que no hay una diferencia significativa para la persona típica. (Por expertos, se refiere a profesionales de la ciencia del color o fotógrafos, diseñadores, profesionales de la imagen experimentados, etc.)
En resumen, hemos aprendido cómo usar números para definir colores y la razón detrás de ello. También identificamos las diferencias entre cada espacio de color, como XYZ y L*a*b*. Y, por último, aprendimos formas de medir el color y cómo definir las diferencias de color. Usando los valores delta E * 00, podemos juzgar si el color es exacto o no.

Figura 6-1: Tabla X-rite Classic ColorChecker

Figura 6-2: Tabla X-rite Digital ColorChecker SG